2.1.0 Razinom okidani bistabili

Slika 2.1-1(a) prikazuje blok dijagram SR bistabila. Ima dva ulaza, označena sa S i R, i dva izlaza, označena s Q i . Slika 2.1-1(b) prikazuje izvedbu SR bistabila korištenjem NILI vratiju. Funkcionalna tablica istinitosti SR bistabila je prikazana na slici 2.1-1(c). Može se uočiti da su za ulaznu kombinaciju S = 0 i R = 0, izlazi Q = Q_p i =, pri čemu indeks p označuje prethodna stanja od Q i . To znači da se za navedenu ulaznu kombinaciju stanja izlaza ne mijenjaju. Ako su trenutna stanja na izlazu Q = 1 i = 0, pojava stanja 0 na S i R ulazu znači da stanja na izlazima Q i ostaju nepromjenjena. Ako su pak stanja ulaza S = 0 i R = 1, onda se nezavisno od prethodnih vrijednosti na izlazu, stanje izlaza Q postavlja u 0, a stanje izlaza u 1. Ako su pak stanja na ulazima S = 1 i R = 0, onda su odgovarajuća stanja izlaza nezavisno od prethodnim vrijednostima ulaza Q = 1, a = 0. Ulazna kombinacija S = 1 i R = 1 nije dozvoljena jer postavlja Q i u stanje nule što je suprotno činjenici da stanja izlaza uvijek moraju biti komplementarna.

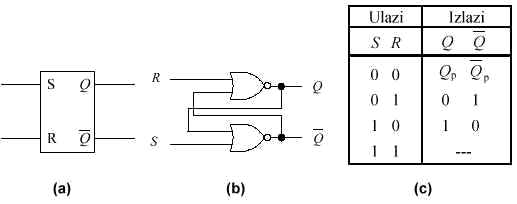
Slika 2.1 -1 SR bistabil: (a) blok dijagram, (b) logička izvedba i (c) tablica istinitosti

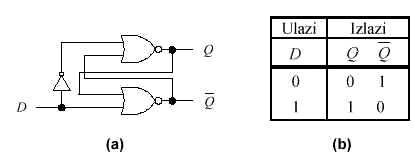
Slika 2.1-2 D bistabil: (a) logička izvedba i (b) tablica istinitosti

Nepoželjno stanje Q = = 0 izbjegava se zabranom istovremenog postavljanja ulaza u stanje 1. To se postiže D bistabilom, modificiranim SR bistabilom, prikazanim na slici 2.1-2(a). Funkcionalna tablica istinitosti D bistabila je prikazana na slici 2.1-2(b). Kod D bistabila stanje izlaza Q uvijek slijedi stanje ulaza D bistabila te se taj element naziva elementom za kašnjenje.

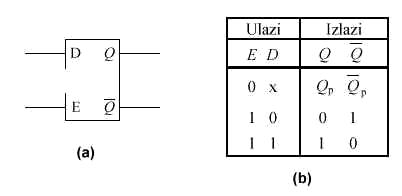
Slika 2.1-3 D bistabil s E ulazom : (a) blok dijagram i (b) tablica istinitosti (x = 0 ili 1)

Slika 2.1-3(a) prikazuje blok dijagram D bistabila s dodatnom upravljačkom ulaznom linijom E koja dozvoljava ili zabranjuje promjene stanja bistabila, odnosno određuje trenutak promjene stanja na izlazu. Kada je stanje na ulazu E = 1 bistabil će se ponašati kao element za kašnjenje, dok se u slučaju kada je E = 0 stanje izlaza neće mijenjati, što je prikazano funkcionalnom tablicom istinitosti na slici 2.1-3(b). Integrirani krug 74’100 predstavlja primjer D bistabila.

Kod analize digitalnih mreža koje sadrže memorijske elemente prikladno je grafički prikazati ulazne i izlazne signale u vremenu pomoću vremenskog dijagrama. Dogovorno se pozitivne vrijednosti napona, +V, pridružuju vrijednosti logičke 1, a vrijednost 0 V vijednosti logičke 0. Na slici 2.1-4 prikazani su vremenski dijagrami za SR i D bistabil. Iz vremenskog dijagrama SR bistabila je vidljivo da se stanja na izlazima Q i mijenjaju kada na ulazima S i R postoji stanje koje dovodi do njihove promjene. Iz vremenskog dijagrama za D bistabil s ulazom E je vidljivo da će stanje na izlazu Q slijediti stanje na ulazu D samo kada je signal E = 1.

Slika 2.1-4 Primjer vremenskog dijagrama: (a) za SR bistabil; (b) za D bistabil

povratak